FUNCIONES EXPONENCIALES Y LOGARÍTMICAS

FUNCIÓN EXPONENCIAL 

Recordemos las Leyes de Exponentes:

        i)    a^x. a^y = a^x+y                                    ii)    a^x/a^y = a^x-y

       iii)    a⁰ = 1                                                                     iv)   (a^x)^y  = a^xy

        v)    (a.b)^x = a ^x.b ^x

La funciones exponenciales son expresadas de esta forma: 

y = f(x) = a^x

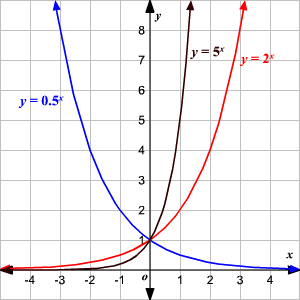
Donde a siempre será un numero real positivo y de esta dependerá el comportamiento de la gráfica de la función. Si a>1 la gráfica será creciente y si, por el contrario, está en el siguiente intervalo 0 < a <1, la gráfica será decreciente.

¹

De las siguientes gráficas podemos deducir que el dominio, los valores que tomarán en x, tenderán siempre el infinito positivo al negativo, por lo que podemos asumir que tomará los reales

Dom f = R

Mientras que su rango, los valores que se tomarán en y, .serán siempre positivos y sin incluir al 0, osea 

Ran f = <0, +∞>

Hemos preparado ejercicios adicionales para mayor entendimiento del tema, esté es el enlace al archivo: formato pdf

FUNCIÓN LOGARÍTMICA

Las funciones logarítmicas son expresadas de la siguiente forma: 

y = f(x) = log_ax

Por lo tanto: 

x= a^y

Teniendo en cuenta eso, es necesario saber que "a" solo puede tomar los valores positivos diferentes a 1 y 0. Existen 2 tipos de sistemas de logaritmos, los logaritmos comunes que tiene como base al numero 10:

log₁₀(z) = log(z)

Y los logaritmos naturales, o neperianos, tienen como base al numero e=2.7182818...

log_e(z) = ln(z)

²

De las siguientes gráficas podemos deducir que el dominio, los valores que tomarán en x, serán siempre positivos y sin incluir al 0, osea 

Dom f = <0, +∞>

Mientras que su rango, los valores que se tomarán en y, tenderán siempre el infinito positivo al negativo, por lo que podemos asumir que tomará los reales.

Ran f = R

Al igual que con el tema de funciones exponenciales, preparamos ejercicios adicionales de funciones logarítmicas, esté es el enlace al archivo: formato pdf
Y también mencionarles que Jhon Quispe, un integrante de nuestro grupo, ha realizado un video donde explicará un ejercicio en concreto relacionando con el tema, aquí el video:

Archivo con resolución del video: formato pdf

Además, para mayor entendimiento del tema, hemos preparado un archivo con ejercicios de aplicación en el siguiente link: 

¹Fuente: imagen de funcion exponenciales
²Fuente: imagen de funcion logaritmica